QUÍMICA

DIAGRAMAS EPÓNIMOS DE LA QUÍMICA

 diagrama de Eadie-Hofstee, también llamado de Woolf-Eadie-Augustinsson-Hofstee o de Eadie-Augustinsson, es una representación gráfica de la función matemática utilizada en bioquímica en el estudio de la cinética de las reacciones enzimáticas, por la que se relaciona la velocidad de una reacción con la concentración del sustrato:

${\displaystyle v=-K_{m}{v \over [S]}+v_{max}}$

donde 'v' representa la velocidad de la reacción, 'K_m' es la constante de Michaelis-Menten, [S] es la concentración del sustrato y 'v_max' es el máximo de la velocidad de la reacción.

El diagrama puede deducirse de la ecuación de Michaelis-Menten como sigue:

${\displaystyle v={{v_{max}[S]} \over {K_{m}+[S]}}}$

si se invierte y multiplica por ${\displaystyle v_{max}}$, se obtiene:

${\displaystyle {v_{max} \over v}={{v_{max}(K_{m}+[S])} \over {v_{max}[S]}}={{K_{m}+[S]} \over {[S]}}}$

que reordenando:

${\displaystyle v_{max}={{{vK_{m}} \over {[S]}}+{{v[S]} \over {[S]}}}={{vK_{m}} \over {[S]}}+v}$

al aislar v se obtiene:

${\displaystyle v=-K_{m}{v \over {[S]}}+v_{max}}$

De manera similar a otras técnicas que linealizan la ecuación de Michaelis-Menten, el diagrama de Eadie-Hofstee permite visualizar rápidamente los parámetros cinéticos importantes como K_m y v_max, pero está menos afectado por el margen de error que el diagrama de Lineweaver-Burk, debido a que asigna el mismo peso a todos los puntos para cualquier concentración del sustrato o velocidad de reacción.

Una de las consecuencias del planteamiento de Eadie-Hofstee es que las variables en la ordenada y en la abscisa no son independientes, sino que ambas dependen de la velocidad de reacción. En consecuencia, cualquier error experimental se manifiesta en ambos ejes.

Los diagramas de Tanabe-Sugano son usados en la química de coordinación para predecir las absorciones en el UV-Visible e IR de compuestos de coordinación. Estos diagramas permiten hacer un cálculo aproximado de la energía de desdoblamiento del campo ligando (10dq o Δ_o) que puede ser comparada con los resultados experimentales. Estos diagramas funcionan tanto para complejos de alto espín como de bajo espín, a diferencia de los diagramas de Orgel que solo funcionan para complejos de alto espín.

Esquema del diágrama de Tanabe-Sugano (rotulado en alemán)

Historia[editar]

Cuando Yukito Tanabe y Satoru Sugano publicaron su artículo sobre los espectros de absorción de complejos iónicos, había poca información sobre los estados electrónicos de complejos metálicos. Ellos usaron la teoría de campo cristalino de Hans Bethe y las combinaciones lineales de Giulio Racah,¹​ para determinar los ahora llamados parámetros de Racah que servían para explicar los espectros de absorción de compuestos octaédricos de una mejor manera que la existente.²​ Estimaron los valores de los parámetros de Racah B y C, para cada configuración electrónica basada en los espectros absorción de los metales del primer grupo (metales Alcalinos). Las gráficas de las energías calculadas para cada estado de transición son conocidas como los diagramas de Tanabe-Sugano.³​⁴​

Parámetros[editar]

Dado que estos diagramas consideran la correlación que existe entre los estados de alto y bajo espín, es necesario incluir todos los estados del sistema. Además para hacerlos generales habremos de incluir algunos otros parámetros. Tomando en cuenta que la repulsión electrónica es la responsable de las diferencias energéticas entre los estados espectroscópicos, es necesario expresarla por medio de algunos parámetros que hablen de ella, estos no son más que combinaciones lineales de algunas integrales de Coulomb y de intercambio, y se les conoce como los parámetros de Racah B y C. Estos, a pesar de poder obtenerse numéricamente, en general se evalúan empíricamente a partir de los espectros de los iones libre. A continuación se presentan una tabla con los valores de B y C para un grupo de metales de transición.⁵​

Carga →	0	0	+1	+1	+2	+2	+3	+3	+4	+4
Elemento ↓	B	B/C	B	B/C	B	B/C	B	B/C	B	B/C
Ti	560	3.3	680	3.7	720	3.7
V	580	3.9	660	4.2	765	3.9	860	4.8
Cr	790	3.2	710	3.9	830	4.1	917	4.5	1040	4.1
Mo	460	3.9	440	4.5
W	370	5.1
Mn	720	4.3	870	3.8	860	3.5	680
Re	850	3.4	470	4.0			1140	3.2
Fe	805	4.4	870	4.2	1060	4.1
Ru	600	5.4	670	3.5	620	6.5
Co	780	5.3	880	4.4	1120	3.9
Ni	1025	4.1	1040	4.2	1080	4.5
Pd					830	3.2
Cu			1220	4.0	1240	3.8

Para obtener las diferencias de energía entre los estados de diferente multiplicidad, se requieren ambos parámetros B y C (por ejemplo, la diferencia entre las energías entre el ⁴F y el ²G es 4B+ 3C) y para caracterizar los estados de la misma multiplicidad, el parámetro B basta. Entonces los diagramas de Tanabe-Sugano se presentan como gráficas de la energía de separación en términos de 10dq, pero expresados en unidades de E/B y 10dq/B respectivamente.⁶​

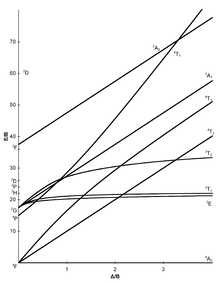
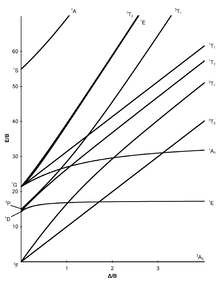
En los diagramas de Tanabe-Sugano, el estado de mínima energía es el eje X, este eje expresado en términos del parámetro de desdoblamiento del campo ligando ( 10dq o Δ_o) dividido entre el parámetro de Racah (B). consecuentemente, la distancia vertical sobre el eje es una medida de la energía sobre el estado basal. Por ejemplo, en un sistema d², el estado de mínima energía es descrito por la línea en el diagrama de correlación uniendo el estado ³T_1g del término ³F con el ³T_1g del término t_2g². En el diagrama de Tanabe-Sugano (figura abajo), esta línea es horizontal y se etiqueta como ³T_1g(F), surgiendo del término ³F en el límite de ion libre (la F entre paréntesis distingue este término ³T_1g del término de mayor energía ³T_1g que surge del término ³P).⁷​

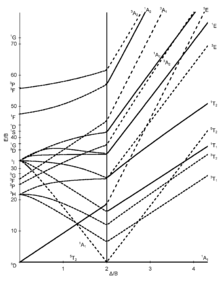
El eje Y está expresado en términos de la energía del estado excitado dividido sobre el parámetro de Racah (E/B), los estados de misma multiplicidad de espín que el estado basal están representados por cada una de las bandas transversales en los diagramas, (son las transiciones posibles por espín) los estados excitados de otra multiplicidad se muestran pero por lo regular no son importantes en la interpretación y esto se debe a que las Transiciones a estados excitados de misma multiplicidad son más probables que de distinta multiplicidad. Para enfatizarlo, En algunos se muestra el estado basal y los estados excitados de misma multiplicidad que el basal se muestran como líneas gruesas, mientras que estados con multiplicidades distintas, se muestran como líneas punteadas. A continuación se muestra las representaciones irreducibles de cada término.⁷​

Término	Degeneración	estados
S	1	A1g
P	3	T1g
D	5	Eg + T2g
F	7	A2g + T1g + T2g
G	9	A1g + Eg + T1g + T2g
H	11	Eg + T1g + T1g + T2g
I	13	A1g + A2g + Eg + T1g + T2g + T2g

Diagramas de Tanabe-Sugano[editar]

Configuración electrónica d2	Configuración electrónica d3	Configuración electrónica d4	Configuración electrónica d5
Configuración electrónica d6	Configuración electrónica d7	Configuración electrónica d8

Diagramas T-S para d1, d9, d10[editar]

No hay necesidad de diagramas de T-S para sistemas d¹, ya que solamente se observará una banda de transición. El término d² se divide en los estados ²T_2g y ²E_g, con una transición correspondiente a ²T_2g a ²E_g, lo que está de acuerdo a la única banda observada en el d⁹ la transición es al revés, para un d¹⁰ no hay transiciones d-d, pues están llenos los orbitales.

transición electrónica para un d1

transición electrónica para un d9

distorsión por el efecto Jahn Teller

De acuerdo con esto para un d¹ o d⁹ esperaríamos solamente una banda correspondiente a la excitación del nivel t_2g al e_g. Sin embargo, los espectros muestran, aparentemente, 2 bandas cercanas traslapándose para [Ti(H₂O)₆]⁺³ (d¹) y para [Cu(H₂O)₆]⁺² (d⁹). La respuesta se encuentra en el hecho de que ambas moléculas sufren distorsión en sus geometrías octaédricas ideales por el efecto Jahn-Teller;⁸​ teniendo estados electrónicos degenerados, se distorsionan para reducir la degeneración (O_h → D_4h). Otras configuraciones (como d⁴) pueden presentar también el mismo efecto.

En general, los diagramas de Tanabe-Sugano asumen geometrías octaédricas en los estados basal y excitados. La mayoría de los sistemas se comportan de esta manera. Pero las distorsiones a geometrías ideales son comunes y por consecuencia pueden ocurrir divisiones en las bandas o, en situaciones de distorsiones severas, las bandas serán difíciles de interpretar (d⁵, d⁶, d⁷, d⁸).

Aplicaciones de los diagramas[editar]

El espectro de absorción puede usarse para determinar la magnitud de Δ_o para complejos octaédricos. La precisión estará limitada por las herramientas matemáticas empleadas en la resolución del problema. Los espectros de absorción tienen frecuentemente bandas sobrepuestas, lo que requiere de una técnica matemática (desconvolución) adecuada para reducir las bandas sobrepuestas en sus componentes individuales. Podemos obtener Δ_o y a veces el parámetro de Racah con precisión simplemente usando las posiciones de los máximos de absorción tomados directamente del espectro.

La facilidad con que se puede determinar Δ_o depende de la configuración dⁿ del metal; en algunos casos, Δ_opuede leerse fácilmente del espectro, en otros un análisis más complicado es necesario.

Diagramas d¹, d⁴ (hs), d⁶ (hs), d⁹[editar]

En cada caso hay un estado excitado de misma multiplicidad de spin que el estado basal. Por tanto, hay solo una absorción permitida por spin, con la energía de la radiación absorbida igual a Δ_o.

Diagramas d³, d⁸[editar]

Estas configuraciones tienen un término de estado basal F. En un campo octaédrico, el término F se divide en tres términos: A_2g, T_2g y T_1g. A₂ es el término de menor energía para d³ o d⁸. Para estas configuraciones, la diferencia en energía entre los dos términos de menor energía es Δ_o (es decir la transición ⁴A_{2 →}⁴T₂ para un d³ y un d^{8 3}A_{2 →}³T₂ . Por tanto, para encontrar Δ_o simplemente encontramos la energía de la transición de mínima energía en el espectro de absorción.

Diagramas d², d⁷ (hs)[editar]

Uno querría simplemente tomar el valor de la transición ³T_1g → ³T_2g y asignarla a Δ_o (después de todo, ³T_1g (F) es t_2g y ³T_2g es e_g, y la diferencia DEBERÍA ser Δ_o). Sin embargo, debido a que el mezclado de ³T_1g(F) y ³T_1g(P) causa una curvatura en ambas líneas, llevaría a un error si empleáramos el estado basal para obtener Δ_o.

transiciones para un d2

Para obtener un valor más exacto es necesario calcular el parámetro de Racah B, el primer paso es calcular la relación que hay entre las dos absorciones que aparecen en el espectro UV-Visible (V₂ / V₁ el cual debe ser mayor a 1), el segundo paso es encontrar la posición en el eje X de diagrama de Tanabe-Sugano donde la relación entre la distancia que hay entre la línea del estado basal a ³T_1g y del estado basal a ³T_2g (para un d2) sea igual a la relación V2 / V1. A continuación se muestra una tabla que se puede utilizar para hacer este cálculo para un d2 .⁹​

Δo/ B	V1(cm)	V2(cm)	V2 / V1
5	0.5	1	2
10	1.1	2	1.82
15	1.6	2.7	1.67
20	2.2	3.6	1.64
25	2.9	4.4	1.52
30	3.5	4.9	1.40
35	4	5.5	1.38
40	4.6	6	1.30

Una vez que se analizó que en parte de Δo / B se encuentra esta relación lo siguiente es sustituir los valores correspondientes del eje Y en la expresión Y= E / B donde E es el valor de la absorción de V₂ y V₁ y así poder calcular el parámetro de Racah B como un promedio de los dos valores obtenidos.

Diagramas d⁵ (hs), d⁴ - d⁷ (ls)[editar]

d⁵ (hs) no tiene estados excitados de la misma multiplicidad. Las bandas de absorción son transiciones prohibidas por spín y son débiles. . Para configuraciones d⁴ – d⁷ (ls) el análisis es difícil ya que hay muchos estados excitados de misma multiplicidad que el estado basal.