QUÍMICA

EPÓNIMOS RELACIONADOS CON LA QUÍMICA

cinética de Michaelis-Menten describe la velocidad de reacción de muchas reacciones enzimáticas. Recibe este nombre en honor a Leonor Michaelis y Maude Menten. Este modelo sólo es válido cuando la concentración del sustrato es mayor que la concentración de la enzima, y para condiciones de estado estacionario, es decir, cuando la concentración del complejo enzima-sustrato es constante.

Determinación de constantes[editar]

Para determinar la velocidad máxima de una reacción enzimática, la concentración de sustrato, ([S]) se aumenta hasta alcanzar una velocidad constante, de formación de producto. Esa es la velocidad máxima (V_max) de la enzima. En ese caso, los sitios activos de la enzima están saturados con sustrato.

Diagrama de velocidad de reacción y constante de Michaelis-Menten.

Velocidad de reacción[editar]

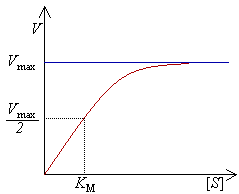
La velocidad V indica el número de moléculas del sustrato que se convierten en producto por segundo. Con concentraciones crecientes de sustrato[S], la enzima va acercándose asintóticamente a su velocidad máxima V_max, pero nunca la alcanza. Por esta razón, no hay un valor de [S] determinado para la V_max. De todas formas, se puede definir un parámetro característico de la enzima empleando la concentración de sustrato a la cual se alcanza la mitad de la velocidad máxima (V_max/2).

Constante de Michaelis[editar]

Artículo principal: Constante de Michaelis-Menten

Aunque es imposible medir exactamente la concentración de sustrato que da V_max, las enzimas pueden caracterizarse mediante la concentración de sustrato a la cual la velocidad de reacción es la mitad de la velocidad máxima. Esta concentración de sustrato se conoce como constante de Michaelis-Menten (K_M).

Para enzimas que exhiben una cinética de Michaelis-Menten simple esta constante representa la constante de disociación del complejo enzima-sustrato (ES) (o la inversa de la afinidad entre enzima y sustrato). Valores bajos indican que el complejo ES está unido muy fuertemente y raramente se disocia sin que el sustrato reaccione para dar producto.

En estos casos se obtendrá una K_M diferente según el sustrato específico sobre el que actúe la enzima (como sucede en el caso de enzimas que actúan sobre sustratos análogos) y según las condiciones de reacción en que se realicen las mediciones.

Nota: K_M solo se puede usar para determinar la afinidad de una enzima por un sustrato k₂ es limitante de la velocidad, por ejemplo, k₂ << k₁ y K_M se convierte en k_-1/k₁. Generalmente, k₂ >> k₁ o bien k₂ y k₁ son comparables.

Nelson, DL., Cox, MM. (2000) Lehninger Principles of Biochemistry, 3rd Ed., Worth Publishers, USA

Ecuación[editar]

La derivación de Michaelis y Menten está descrita por Briggs y Haldane. Se obtiene de la siguiente manera:

Se supone que la reacción enzimática es irreversible, y que el producto no se liga con la enzima después de la reacción.

${\displaystyle E+S{\begin{matrix}k_{1}\\\longrightarrow \\\longleftarrow \\k_{-1}\end{matrix}}ES{\begin{matrix}k_{2}\\\longrightarrow \\\ \end{matrix}}E+P}$

Siguiendo la aproximación del estado estacionario, que señala que la concentración del complejo enzima-sustrato (${\displaystyle ES}$) es pequeña y se mantiene casi constante a lo largo de la reacción enzimática:

${\displaystyle {\frac {d[ES]}{dt}}=k_{1}[E][S]-k_{-1}[ES]-k_{2}[ES]=0}$

${\displaystyle [ES]={\frac {k_{1}[E][S]}{k_{-1}+k_{2}}}}$

Se define:

${\displaystyle K_{m}={\frac {k_{-1}+k_{2}}{k_{1}}}}$

Entonces:

${\displaystyle [ES]={\frac {[E][S]}{K_{m}}}}$ (1)

La velocidad de reacción es:

${\displaystyle {\frac {d[P]}{dt}}=k_{2}[ES]}$ (2)

La concentración total de la enzima:

${\displaystyle [E_{0}]=[E]+[ES]}$

Por lo tanto:

${\displaystyle [E]=[E_{0}]-[ES]}$ (3)

Sustituyendo (3) en (1) da:

${\displaystyle [ES]={\frac {([E_{0}]-[ES])[S]}{K_{m}}}}$

Reordenando:

${\displaystyle K_{m}[ES]+[S][ES]=[E_{0}][S]}$

${\displaystyle [ES]={\frac {[E_{0}][S]}{K_{m}+[S]}}}$ (4)

Sustituyendo (4) en (2) :

${\displaystyle {\frac {d[P]}{dt}}=k_{2}[E_{0}]{\frac {[S]}{K_{m}+[S]}}=V_{max}{\frac {[S]}{K_{m}+[S]}}}$

Esta ecuación se puede analizar experimentalmente con un diagrama de Lineweaver-Burke, un diagrama de Eadie-Hofstee o un diagrama de Hanes-Woolf.

• ${\displaystyle E_{0}}$ es el total de enzima. No es práctico medir la cantidad de complejo enzima-sustrato durante la reacción, por lo que debe escribirse ésta en términos de cantidad total o inicial de enzima, que es una cantidad conocida.
• ${\displaystyle d[P]/dt}$ o ${\displaystyle V_{0}}$ es la velocidad de formación del producto.
• ${\displaystyle k_{2}[E_{0}]}$ o ${\displaystyle V_{max}}$ es la velocidad máxima. k₂ se denomina con frecuencia k_cat.

Cabe observar que [S] es grande comparada con K_m, [S]/(K_m + [S]) tiende a 1. La velocidad de formación de producto es igual a k₂[E₀] en ese caso.

Cuando [S] es igual a K_m, [S]/(K_m + [S]) vale 0.5. En ese caso, la velocidad de formación de producto es la mitad de la máxima (1/2 V_max). Representando gráficamente V₀ frente a [S] se puede fácilmente determinar V_max y K_m. Esto requiere una serie de experimentos a E₀ constante y diferentes concentraciones de sustrato [S].

Amedeo Avogadro, Conde de Quaregna y Cerreto (Turín, 9 de agosto de 1776 - Turín, 9 de julio de 1856), fue un físico y químico italiano, profesor de Física de la Universidad de Turín desde 1820 hasta su muerte.

Valor de NA1​	Unidad
6,022 140 857(74) × 1023	mol−1
2,731 597 34(12) × 1026	(lb-mol)−1
1,707 248 434(77) × 1025	(oz-mol)−1

La constante de Avogadro (símbolos: L, N_A) es el número de partículas constituyentes (usualmente átomos o moléculas) que se encuentran en la cantidad de sustancia de un mol. Por tanto, es el factor proporcional que relaciona la masa molar de una sustancia a la masa de una muestra. Su valor es igual a 6,022 140 857(74) ×10²³ mol⁻¹.²​³​⁴​

Definiciones anteriores de cantidad química involucraron el número de Avogadro, un término histórico íntimamente relacionado a la constante de Avogadro pero definida de otra forma: inicialmente definido por Jean Baptiste Perrin como el número de átomos en un mol de hidrógeno. Luego fue redefinido como el número de átomos en 12 gramos del isótopo carbono-12 y posteriormente generalizado para relacionar cantidades de sustancias a sus pesos moleculares.⁵​ Por ejemplo, de forma aproximada, 1 gramo de hidrógeno, que tiene un número másico de 1, contiene 6,022 × 10²³ átomos de hidrógeno, es decir, más de seiscientos mil trillones de átomos. De igual manera, 12 gramos de carbono-12 (número másico 12) contienen el mismo número de átomos, 6,02214 × 10²³. El número de Avogadro es una magnitud adimensional y tiene el valor numérico de la constante de Avogadro, que posee unidades de medida.

La constante de Avogadro es fundamental para entender la composición de las moléculas y sus interacciones y combinaciones. Por ejemplo, ya que un átomo de oxígeno se combinará con dos átomos de hidrógeno para crear una molécula de agua (H₂O), de igual forma un mol de oxígeno (6,022 × 10²³ átomos de O) se combinará con dos moles de hidrógeno (2 × 6,022 × 10²³ átomos de H) para crear un mol de H₂O.

Revisiones en el conjunto de las unidades básicas del SI hicieron necesario redefinir los conceptos de cantidad química, por lo que el número de Avogadro y su definición fueron reemplazados por la constante de Avogadro y su definición. Se ha propuesto que cambios en las unidades SI fijaran de manera precisa el valor de la constante a exactamente 6,02214×10²³ al expresarla en la unidad mol⁻¹ (véase Redefinición de las unidades del SI; la X al final de un número significa que uno o más dígitos finales poseen cierta incertidumbre).

Historia[editar]

La constante de Avogadro debe su nombre al científico italiano de principios del siglo XIX Amedeo Avogadro, quien, en 1811, propuso por primera vez que el volumen de un gas (a una determinada presión y temperatura) es proporcional al número de átomos, o moléculas, independientemente de la naturaleza del gas.⁶​ El físico francés Jean Perrin propuso en 1909 nombrar la constante en honor de Avogadro.⁷​ Perrin ganó en 1926 el Premio Nobel de Física, en gran parte por su trabajo en la determinación de la constante de Avogadro mediante varios métodos diferentes.⁸​

El valor de la constante de Avogadro fue indicado en primer lugar por Johann Josef Loschmidt que, en 1865, estimó el diámetro medio de las moléculas en el aire por un método equivalente a calcular el número de partículas en un volumen determinado de gas.⁹​ Este último valor, la densidad numérica de partículas en un gas ideal, que ahora se llama en su honor constante de Loschmidt, es aproximadamente proporcional a la constante de Avogadro. La conexión con Loschmidt es la raíz del símbolo L que a veces se utiliza para la constante de Avogadro, y la literatura en lengua alemana puede referirse a ambas constantes con el mismo nombre, distinguiéndolas solamente por las unidades de medida.¹⁰​

Terminología y unidades[editar]

Originalmente se propuso el nombre de "número de Avogadro" para referirse al número de moléculas en una molécula-gramo de oxígeno (exactamente 32 gramos de dioxígeno (antiguamente oxígeno), de acuerdo con las definiciones del periodo),⁷​ y este término es aún ampliamente utilizado, especialmente en la introducción de los trabajos. Véase, por ejemplo.¹¹​ El cambio de nombre a "constante de Avogadro" vino con la introducción del molcomo una unidad básica separada dentro del Sistema Internacional de Unidades (SI) en 1971,¹²​ que reconoció la cantidad de sustancia como una unidad independiente.¹³​ Con este reconocimiento, la constante de Avogadro ya no es un número puro, sino una magnitud física, asociada con una unidad de medida, la inversa de mol (mol^-1) en unidades SI.¹³​ El cambio de nombre de la forma posesiva "de Avogadro" a la forma nominativa "Avogadro" es un cambio general en práctica desde la época de Perrin para los nombres de todas las constantes físicas.¹⁴​ En efecto, la constante es nombrada en honor de Avogadro: no se refiere al propio Avogadro, y habría sido imposible medirla durante la vida de Avogadro.

Los dígitos entre paréntesis al final del valor de la constante de Avogadro se refieren a su incertidumbre estándar, concretamente el valor 0,000 000 27×10²³ mol⁻¹. Si bien es raro el uso de unidades de cantidad de sustancia distintas del mol, la constante de Avogadro también se puede definir en unidades como la libra-mol (lb-mol) y la onza-mol (oz-mol).

N_A = 6,022 141 29(27)×10²³ mol⁻¹ = 2,731 597 57(14)×10²⁶ lb-mol⁻¹ = 1,707 248 479(85)×10²⁵ oz-mol⁻¹

Relaciones físicas adicionales[editar]

Debido a su papel como factor de escala, la constante de Avogadro establece un vínculo entre una serie de útiles constantes físicas cuando nos movemos entre la escala atómica y la escala macroscópica. Por ejemplo, establece la relación entre:

• la constante de los gases R y la constante de Boltzmann k_B (en J mol⁻¹ K⁻¹):

${\displaystyle R=k_{\rm {B}}N_{\rm {A}}=8.314\,472(15)\ {\rm {J\,mol^{-1}\,K^{-1}}}\,}$

• la constante de Faraday F y la carga elemental e (en C mol⁻¹):

${\displaystyle F=N_{\rm {A}}e=96\,485.3383(83)\ {\rm {C\,mol^{-1}}}\,}$

La constante de Avogadro también entra en la definición de la constante de masa atómica (m_u):

${\displaystyle m_{\rm {u}}={\frac {M_{\rm {u}}}{N_{\rm {A}}}}=1.660\,538\,782(83)\times 10^{-24}\ {\rm {g}}}$

donde M_u es la constante de masa molar.

Medida[editar]

Coulombimetría[editar]

El primer método preciso de medir el valor de la constante de Avogadro se basaba en la culombimetría. El principio consiste en medir la constante de Faraday, F, que es la carga eléctrica transportada por un mol de electrones, y dividir por la carga elemental, e, para obtener la constante de Avogadro.

${\displaystyle N_{\rm {A}}={\frac {F}{e}}}$

El experimento clásico es el de Bowers y Davis en el NIST,¹⁵​ y se basa en la disolución de la plata del ánodo de una celda electrolítica, al pasar una corriente eléctrica constante I durante un tiempo conocido t . Si m es la masa de plata perdida por el ánodo y A_r el peso atómico de la plata, entonces la constante de Faraday viene dada por:

${\displaystyle F={\frac {A_{\rm {r}}M_{\rm {u}}It}{m}}}$

Los investigadores del NIST desarrollaron un ingenioso método para compensar la plata que se perdía desde el ánodo por razones mecánicas, y realizó un análisis isotópico de su plata para determinar el peso atómico apropiado. Su valor para la convencional constante de Faraday es: F₉₀ = 96485,309 C/mol, que corresponde a un valor para la constante de Avogadro de 6,0221367·10²³ mol⁻¹: ambos valores tienen una incertidumbre estándar relativa de 1.3. 10^-6.

Método de la masa de electrones[editar]

Committee on Data for Science and Technology (CODATA, Comité de Información para Ciencia y Tecnología) publica regularmente los valores de las constantes físicas para su uso internacional. En el caso de la constante de Avogadro,¹⁶​ la determina a partir del cociente entre la masa molar del electrón A_r(e), M_u y la masa en reposo del electrón m_e:

${\displaystyle N_{\rm {A}}={\frac {A_{\rm {r}}({\rm {e}})M_{\rm {u}}}{m_{\rm {e}}}}}$

La "masa atómica relativa" del electrón, A_r(e), es una cantidad medible directamente, y la constante masa molarM_u, es una constante definida en el sistema SI. La masa en reposo del electrón, sin embargo, se calcula a partir de otras constantes medidas:¹⁶​

${\displaystyle m_{\rm {e}}={\frac {2R_{\infty }h}{c\alpha ^{2}}}}$

Como puede observarse en los valores de la tabla CODATA 2006,¹⁴​ el principal factor limitante en la precisión con la que se conoce el valor de la constante de Avogadro es la incertidumbre en el valor de la constante de Planck, ya que todas las demás constantes que contribuyen al cálculo se conocen con mucha más precisión.

Constante	Símbolo	Valor 2006 CODATA	Incertidumbre estándar relativa	Coeficiente de correlación con NA
Masa atómica relativa del electrón	Ar(e)	5,485 799 0943(23)×10-4	4.2. 10–10	0,0082
Constante de masa molar	Mu	0,001 kg/mol	definida	—
Constante de Rydberg	R∞	10 973 731,568 527(73) m−1	6,6×10-12	0,0000
Constante de Planck	h	6,626 068 96(33)×10-34 Js	5,0×10-8	–0,9996
Velocidad de la luz	c	299 792 458 m/s	definida	—
Constante de estructura fina	α	7,297 352 5376(50)×10-3	6,8×10-10	0.0269
Constante de Avogadro	NA	6,022 141 79(30)×1023 mol−1	5,0×10-8	1

Método de la densidad del cristal por rayos X[editar]

Modelo de bolas y varillas de la celda unidad de silicio. Experimentos de difracción de rayos X pueden determinar el parámetro de la celda,a, que a su vez puede utilizarse para calcular el valor de la constante de Avogadro.

Un método moderno para calcular la constante de Avogadro es utilizar la relación del volumen molar, V_m, al volumen de la celda unidad, V_cell, para un cristal sencillo de silicio:¹⁷​

${\displaystyle N_{\rm {A}}={\frac {8V_{\rm {m}}({\rm {Si}})}{V_{\rm {cell}}}}}$

El factor de ocho se debe a que hay ocho átomos de silicio en cada celda unidad.

El volumen de la celda unidad se puede obtener por cristalografía de rayos X; como la celda unidad es cúbica, el volumen es el de un cubo de la longitud de un lado (conocido como el parámetro de la celda unidad, a). En la práctica, las medidas se realizan sobre una distancia conocida como d₂₂₀(Si) que es la distancia entre los planos indicada por el índice de Miller{220}, y es igual a a/√8. El valor CODATA2006 para d₂₂₀(Si) es 192.015 5762(50) pm, con una incertidumbre relativa de 2.8. 10^–8, correspondiente a un volumen de celda unidad de 1.601 933 04(13). 10^–28 m³.

La composición isotópica proporcional de la muestra utilizada debe ser medida y tenida en cuenta. El silicio presenta tres isótopos estables - ²⁸Si, ²⁹Si, ³⁰Si - y la variación natural en sus proporciones es mayor que otras incertidumbres en las mediciones. La Masa atómica A_r para un cristal sencillo, puede calcularse ya que las masas atómicas relativas de los tres núclidos se conocen con gran exactitud. Esto, junto con la medida de la densidad ρ de la muestra, permite calcular el volumen molarV_m que se encuentra mediante:

${\displaystyle V_{\rm {m}}={\frac {A_{\rm {r}}M_{\rm {u}}}{\rho }}}$

dondeM_u es la masa molar. El valor CODATA2006 para el volumen molar del silicio es 12.058 8349(11) cm³/mol, con una incertidumbre estándar relativa de 9.1. 10^–8.¹⁸​

A partir de los valores CODATA2006 recomendados, la relativa incertidumbre en la determinación de la constante de Avogadro por el método de la densidad del cristal por rayos X es de 1,2. 10^-7, cerca de dos veces y media mayor que la del método de la masa del electrón.