QUÍMICA

ECUACIONES EPÓNIMAS DE LA QUÍMICA

ecuación de Arrhenius es una expresión matemática que se utiliza para comprobar la dependencia de la constante de velocidad (o cinética) de una reacción química con respecto a la temperatura a la que se lleva a cabo esa reacción.¹​ La ecuación fue propuesta primeramente por el químico holandés J. H. van 't Hoff en 1884; cinco años después en 1889 el químico sueco Svante Arrhenius dio una justificación física y una interpretación para la ecuación. Actualmente, es vista mejor como una relación empírica.²​ Puede ser usada para modelar la variación de temperatura de coeficientes de difusión, población de vacantes cristalinas, velocidad de fluencia, y muchas otras reacciones o procesos inducidos térmicamente.

Información general[editar]

Dicho de manera breve, la ecuación de Arrhenius da la dependencia de la constante de velocidad ${\displaystyle k}$ de reacciones químicas a la temperatura ${\displaystyle T}$ (en temperatura absoluta, tales como kelvins o grados Rankine) y la energía de activación³​ ${\displaystyle E_{\mathrm {a} }}$, de acuerdo con la expresión:¹​

${\displaystyle k(T)=A{\mathrm {e} }^{-{\frac {E_{\mathrm {a} }}{RT}}}}$

donde:

• ${\displaystyle k(T)}$: constante cinética (dependiente de la temperatura)
• ${\displaystyle A}$: factor preexponencial o factor de frecuencia. Indica la frecuencia de las colisiones.
• ${\displaystyle E_{\mathrm {a} }}$: energía de activación, expresada en J/mol.
• ${\displaystyle R}$: constante universal de los gases. Su valor es 8,3143 J·K^-1·mol^-1
• ${\displaystyle T}$: temperatura absoluta [K]

Gráfico de Arrhenius[editar]

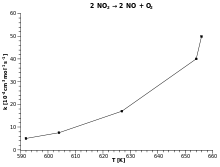
Ejemplo: Decaimiento de dióxido de nitrógeno
2 NO2 → 2 NO + O2
Gráfico convencional: k respecto a T
Gráfico de Arrhenius: ln(k) respecto a 1/T

Para utilizar la ecuación de Arrhenius como modelo de regresión linealentre las variables ${\displaystyle K}$ y ${\displaystyle T^{-1}}$, la ecuación puede ser reescrita como:

${\displaystyle \ln(k)=\ln(A)-{\frac {E_{\rm {a}}}{R}}\left({\frac {1}{T}}\right)}$

Un gráfico de Arrhenius muestra el logaritmo de las constantes cinéticas (${\displaystyle \ln(k)}$ en el eje de las ordenadas en coordenadas cartesianas) graficado con respecto al inverso de la temperatura (${\displaystyle 1/T}$, en el eje de las abcisas). Los gráficos de Arrhenius son ocasionalmente utilizados para analizar el efecto de la temperatura en las tasas de rapidez de las reacciones químicas. Para un único proceso térmicamente activado de velocidad limitada, un gráfico de Arrhenius da una línea recta, desde la cual pueden ser determinados tanto la energía de activación como el factor preexponencial.

Cuando se grafica de la forma descrita anteriormente, el valor de la intersección en el eje y corresponderá a ${\displaystyle \ln(A)}$, y la pendiente de la línea será igual a ${\displaystyle -E_{\rm {a}}/k_{B}}$.

El factor preexponencial, ${\displaystyle A}$, es una constante de proporcionalidad que toma en cuenta un número de factores tales como la frecuencia de colisión y la orientación entre las partículas reaccionantes.

La expresión ${\displaystyle \mathrm {e} ^{-E_{\rm {a}}/RT}}$ representa la fracción de las moléculas presentes en un gas que tienen energía igual o superior a la energía de activación a una temperatura dada.

Ecuación de Arrhenius modificada[editar]

La ecuación de Arrhenius modificada ⁴​ es una extensión de la ecuación de Arrhenius en la que el factor preexponencial ${\displaystyle A}$ es proporcional a ${\displaystyle T^{n}}$:

${\displaystyle k=BT^{n}{\mathrm {e} }^{-{\frac {E_{\mathrm {a} }}{RT}}}}$

donde:

• ${\displaystyle B}$ es una constante independiente de la temperatura
• ${\displaystyle n}$ es una constante

Interpretación cinética de la ecuación de Arrhenius[editar]

Arrhenius argumentó que para que los reactivos se transformen en productos, deben primero adquirir una mínima cantidad de energía, llamada la "energía de activación" E_a. A una cierta temperatura absoluta T, la fracción de las moléculas que tiene una energía cinética mayor que E_a puede ser calculada a partir de la distribución de Maxwell-Boltzmann de la mecánica estadística, y resulta ser proporcional a ${\displaystyle \ {\mathrm {e} }^{-{\frac {E_{\mathrm {a} }}{k_{\mathrm {B} }T}}}}$. El concepto de energía de activación explica la naturaleza exponencial de la relación, y de una forma u otra está presente en todas las teorías cinéticas.

Teoría de las colisiones[editar]

Un ejemplo viene de la "teoría de las colisiones" de las reacciones químicas, desarrollada por Max Trautz y William Lewis en los años 1916-1918. En esta teoría, se supone que las moléculas reaccionan si colisionan con una energía cinética relativa a lo largo de sus líneas de centro, que exceda E_a. Esto lleva a una expresión muy similar a la ecuación de Arrhenius.

Teoría del estado de transición[editar]

Otra expresión parecida a la ecuación de Arrhenius aparece en la "teoría del estado de transición" de las reacciones químicas, formulada por Eugene Wigner, Henry Eyring, Michael Polanyi y M. G. Evans en los años 1930s. Esto toma varias formas, pero una de las más comunes es

${\displaystyle \ k={\frac {k_{\mathrm {B} }T}{h}}{\mathrm {e} }^{-{\frac {\Delta G^{\ddagger }}{RT}}}}$

donde:

• ${\displaystyle \Delta G^{\ddagger }}$ es la energía libre de Gibbs de activación,
• ${\displaystyle k_{\mathrm {B} }}$ es la constante de Boltzmann, y
• ${\displaystyle h}$ es la constante de Planck.

A primera vista esto luce como un exponencial multiplicado por un factor que es lineal en temperatura. Sin embargo, se debe recordar que la energía libre es por sí misma una cantidad dependiente de la temperatura. La energía libre de activación es la diferencia de un término de entalpía y un término de entropía multiplicada por la temperatura absoluta. Cuando todos los detalles son considerados, se termina con una expresión que nuevamente toma la forma de la ecuación exponencial de Arrhenius multiplicada por una función de ${\displaystyle T}$ que varía lentamente. La forma precisa de la dependencia de temperatura depende de la reacción, y puede ser calculada usando fórmulas de la mecánica estadística, que envuelven las funciones de partición de los reactivos y del complejo activado.

Limitaciones de la idea de la energía de activación de Arrhenius[editar]

Tanto la energía de activación de Arrhenius como la constante de velocidad (${\displaystyle k}$) son determinadas experimentalmente, y representan parámetros macroscópicos específicos de la reacción que no están relacionados de manera simple a las energías umbrales y al éxito de las colisiones individuales a nivel molecular. Considérese una colisión particular (una reacción elemental) entre las moléculas A y B. El ángulo de colisión, la energía traslacional relativa, la energía (particularmente la vibracional) interna, todos esos factores determinarán la oportunidad de que la colisión produzca una molécula AB. Las medidas macroscópicas de ${\displaystyle E_{\mathrm {a} }}$ y ${\displaystyle k}$ son el resultado de muchas colisiones individuales con diferentes parámetros de colisión. Para probar las velocidades de reacción a nivel molecular, los experimentos tienen que ser realizados bajo condiciones casi colisionales y este tópico es llamado en ocasiones dinámica de reacciones moleculares.

La ecuación de Callendar–Van Dusen es una ecuación que describe la relación entre la resistencia (R) y la temperatura (t) de termorresistencias de platino (RDT).

La forma larga de la ecuación (ver abajo) fue publicada en 1925 por M.S. Van Dusen:

${\displaystyle R(t)=R(0)[1+A*t+B*t^{2}+(t-100)C*t^{3}].}$

La forma simple fue publicada antes por Callendar, Es generalmente valida solo entre 0°C y 661°C:

${\displaystyle R(t)=R(0)(1+A*t+B*t^{2}).}$

donde las constantes A, B, y C son derivadas desde parámetros determinados experimentalmente α, β, y δ son las mediciones de resistencia hechas a 0°C, 100°C y 260°C.

La ecuación fue encontrada por el físico británico Hugh Longbourne Callender, y fue refinada para mediciones a temperaturas más bajas por M. S. Van Dusen, un químico de la U.S. National Bureau of Standards (ahora conocido como el National Institute of Standards and Technology) en un trabajo publicado en 1925 en la Journal of the American Chemical Society.

La ecuación de Eyring, también conocida como ecuación de Eyring–Polanyi en cinética química, relaciona la velocidad de reacción con la temperatura. Fue desarrollada casi simultáneamente en 1935 por Henry Eyring, M.G. Évans y Michael Polanyi. Esta ecuación es parte de la teoría del estado de transición (o bien, teoría del complejo activado) y equivale de modo trivial a la ecuación de Arrhenius obtenida empíricamente; ambas ecuaciones pueden derivarse fácilmente de la termodinámica estadística en la teoría cinética de gases.¹​

La forma de la ecuación de Eyring–Polanyi recuerda algo a la ecuación de Arrhenius:

${\displaystyle \ k={\frac {k_{\mathrm {B} }T}{h}}\mathrm {e} ^{-{\frac {\Delta G^{\ddagger }}{RT}}}}$

donde:

• ${\displaystyle \Delta G^{\ddagger }}$ es la energía libre de activación.
• ${\displaystyle k_{B}}$ es la constante de Boltzmann.
• ${\displaystyle h}$ es la constante de Planck.

Puede reescribirse como:

${\displaystyle k=\left({\frac {k_{\mathrm {B} }T}{h}}\right)\mathrm {exp} \left({\frac {\Delta S^{\ddagger }}{R}}\right)\mathrm {exp} \left(-{\frac {\Delta H^{\ddagger }}{RT}}\right)}$

Para encontrar la forma lineal de la ecuación de Eyring–Polanyi se parte de:

${\displaystyle \ln {\frac {k}{T}}={\frac {-\Delta H^{\ddagger }}{R}}\cdot {\frac {1}{T}}+\ln {\frac {k_{\mathrm {B} }}{h}}+{\frac {\Delta S^{\ddagger }}{R}}}$

donde:

• ${\displaystyle \ k}$ es la constante de velocidad de la ecuación de velocidad,
• ${\displaystyle \ T}$ es la temperatura absoluta,
• ${\displaystyle \ \Delta H^{\ddagger }}$ es la entalpía de activación,
• ${\displaystyle \ R}$ es la constante de los gases ideales,
• ${\displaystyle \ k_{\mathrm {B} }}$ es la constante de Boltzmann,
• ${\displaystyle \ h}$ es la constante de Planck,
• ${\displaystyle \ \Delta S^{\ddagger }}$ es la entropía de activación.

Una cierta reacción química tiene lugar a diferentes temperaturas y se determinan las velocidades de reacción. La gráfica de ${\displaystyle \ \ln(k/T)}$ versus ${\displaystyle \ 1/T}$ da una línea recta con pendiente ${\displaystyle \ -\Delta H^{\ddagger }/R}$ de la cual puede derivarse la entalpía de activación y de la ordenada en el origen o punto de corte con el eje de ordenadas ${\displaystyle \ \ln(k_{\mathrm {B} }/h)+\Delta S^{\ddagger }/R}$ se deriva la entropía de activación.