Física - Magnitudes físicas

La acutancia de una imagen es el grado de contraste que se observa en el límite entre detalles que difieren por su luminancia o densidad óptica. Cuanto más contrastado sea el límite entre una zona oscura y otra más clara, mayor es la acutancia y con ella la nitidez percibida en la imagen. La definición o resolución de la imagen no crecen cuando aumenta la acutancia, pero sí la capacidad para distinguir los detalles y la sensación subjetiva, que es la de un aumento de definición, de detalle. El sistema perceptivo visual humano es capaz de distinguir detalles más pequeños cuando su contraste es mayor.

Fotografía y percepción del contraste[editar]

La acutancia también describe la capacidad de registro de un observador o de una cámara fotográfica en términos de la definición del contraste percibida.¹​

En este sentido la acutancia puede variar según el tipo de soporte sensible a la luz que emplee dicha cámara, sea de película emulsionada, negativo o sensor CCD de una cámara digital.

análisis dimensional es una herramienta muy poderosa, que permite simplificar el estudio de cualquier fenómeno en el que estén involucradas muchas magnitudes físicas en forma de variables independientes. Su resultado fundamental, el teorema π de Vaschy-Buckingham (más conocido por teorema π) permite cambiar el conjunto original de parámetros de entrada dimensionales de un problema físico por otro conjunto de parámetros de entrada adimensionales más reducido. Estos parámetros adimensionales se obtienen mediante combinaciones adecuadas de los parámetros dimensionales y no son únicos, aunque sí lo es el número mínimo necesario para estudiar cada sistema. De este modo, al obtener uno de estos conjuntos de tamaño mínimo se consigue:

• Analizar con mayor facilidad el sistema objeto de estudio
• Reducir drásticamente el número de ensayos que debe realizarse para averiguar el comportamiento o respuesta del sistema.

El análisis dimensional es la base de los ensayos con maquetas a escala reducida utilizados en muchas ramas de la ingeniería, tales como la aeronáutica, la automoción o la ingeniería civil. A partir de dichos ensayos se obtiene información sobre lo que ocurre en el fenómeno a escala real cuando existe semejanza física entre el fenómeno real y el ensayo, gracias a que los resultados obtenidos en una maqueta a escala son válidos para el modelo a tamaño real si los números adimensionales que se toman como variables independientes para la experimentación tienen el mismo valor en la maqueta y en el modelo real. Así, para este tipo de cálculos, se utilizan ecuaciones dimensionales, que son expresiones algebraicas que tienen como variables a las unidades fundamentales y derivadas, las cuales se usan para demostrar fórmulas, equivalencias o para dar unidades a una respuesta.

Finalmente, el análisis dimensional también es una herramienta útil para detectar errores en los cálculos científicos e ingenieriles. Con este fin se comprueba la congruencia de las unidades empleadas en los cálculos, prestando especial atención a las unidades de los resultados.

Análisis dimensional[editar]

Para reducir un problema dimensional a otro adimensional con menos parámetros, se siguen los siguientes pasos generales:

1. Contar el número de variables dimensionales n.
2. Contar el número de unidades básicas (longitud, tiempo, masa, temperatura, etc.) m
3. Determinar el número de grupos adimensionales. El número de grupos o números adimensionales (${\displaystyle {\Pi }}$)es n - m.
4. Hacer que cada número ${\displaystyle {\Pi }}$ dependa de n - m variables fijas y que cada uno dependa además de una de las n - m variables restantes (se recomienda que las variables fijas sean una del fluido o medio, una geométrica y otra cinemática; ello para asegurar que los números adimensionales hallados tengan en cuenta todos los datos del problema).
5. Cada ${\displaystyle {\Pi }}$ se pone como un producto de las variables que lo determinan elevadas cada una a una potencia desconocida. Para garantizar adimensionalidad deben hallarse todos los valores de los exponentes tal que se cancelen todas las dimensiones implicadas.
6. El número ${\displaystyle {\Pi }}$ que contenga la variable que se desea determinar se pone como función de los demás números adimensionales.
7. En caso de trabajar con un modelo a escala, éste debe tener todos sus números adimensionales iguales a las del prototipo para asegurar similitud.

Aplicaciones del Análisis dimensional[editar]

• Detección de errores de cálculo.
• Resolución de problemas cuya solución directa conlleva dificultades matemáticas insalvables.
• Creación y estudio de modelos reducidos.
• Consideraciones sobre la influencia de posibles cambios en los modelos, etc.

Un ejemplo de Análisis dimensional[editar]

Calculemos mediante Análisis Dimensional la velocidad de un cuerpo en caída libre. Sabemos que dicha velocidad ${\displaystyle v}$ dependerá de la altura ${\displaystyle h}$ y de la gravedad ${\displaystyle g}$. Pero imaginemos que también se nos ocurre decir que la velocidad depende de la masa ${\displaystyle m}$. Una de las bondades del Análisis Dimensional es que es "autocorregible", es decir, el procedimiento, por sí solo, elimina las unidades que no son necesarias.

• Identificar las magnitudes de las variables:

${\displaystyle [v]={\text{m/s}}={\text{LT}}^{-1},\quad [g]={\text{m/s}}^{2}={\text{LT}}^{-2},\quad [h]={\text{m}}={\text{L}},\quad [m]={\text{kg}}={\text{M}}}$

• Formar la matriz

${\displaystyle {\begin{array}{cc}&{\begin{bmatrix}{[h]}&{[g]}&{[v]}&{[m]}\end{bmatrix}}\\{\begin{bmatrix}{\textbf {M}}\\{\textbf {L}}\\{\textbf {T}}\end{bmatrix}}&{\begin{bmatrix}{0}&{0}&{0}&{1}\\{1}&{1}&{1}&{0}\\{0}&{-2}&{-1}&{0}\end{bmatrix}}\end{array}}}$

• Hacer el producto de matrices:

Aquí tenemos que decir que ${\displaystyle \displaystyle \epsilon _{k}}$ se refiere al exponente de la unidad ${\displaystyle \displaystyle k}$, pero eso se verá en pasos sucesivos.

${\displaystyle {\begin{bmatrix}{0}&{0}&{0}&{1}\\{1}&{1}&{1}&{0}\\{0}&{-2}&{-1}&{0}\end{bmatrix}}{\begin{bmatrix}{\epsilon _{h}}\\{\epsilon _{g}}\\{\epsilon _{v}}\\{\epsilon _{m}}\end{bmatrix}}={\begin{bmatrix}{0}\\{0}\\{0}\end{bmatrix}}}$

• Desarrollar el producto de matrices y resolver el sistema de ecuaciones.

Se forma un sistema de ecuaciones. Si nos fijamos, tenemos 4 incógnitas, y sólo 3 ecuaciones, así que para que el sistema pueda ser resuelto, necesitamos tantas incógnitas como ecuaciones. ¿Cómo se subsana el problema? Muy sencillo: se coge un ${\displaystyle \displaystyle \epsilon _{k}}$ cualquiera y le asignamos el valor que queramos, a excepción del 0. En nuestro caso, vamos a tomar ${\displaystyle \displaystyle \epsilon _{v}}$ como ${\displaystyle \displaystyle 1}$.

${\displaystyle \left\{{\begin{array}{rrrrcr}\epsilon _{m}&&&&=&0\\&\epsilon _{h}&+\epsilon _{g}&+\epsilon _{v}&=&0\\&&-2\epsilon _{g}&-\epsilon _{v}&=&0\end{array}}\right.\longrightarrow \quad \left\{{\begin{array}{rrrcrcr}\epsilon _{m}&&&=&0\\&\epsilon _{h}&+\epsilon _{g}&=&-\epsilon _{v}&=&-1\\&&-2\epsilon _{g}&=&\epsilon _{v}&=&1\end{array}}\right.}$

Si aplicamos la solución inicial que hemos propuesto anteriormente (${\displaystyle \displaystyle \epsilon _{v}=1}$), se realizan los sencillos cálculos y llegamos a las soluciones:

${\displaystyle \displaystyle \epsilon _{h}=-1/2}$

${\displaystyle \displaystyle \epsilon _{g}=-1/2}$

${\displaystyle \displaystyle \epsilon _{v}=1}$

${\displaystyle \displaystyle \epsilon _{m}=0}$

• Formar el/los grupos ${\displaystyle \displaystyle \Pi }$

Un grupo ${\displaystyle \displaystyle \Pi }$ es una ecuación adimensional. ¿Cuántos grupos ${\displaystyle \displaystyle \Pi }$ vamos a obtener? Pues si ${\displaystyle \displaystyle m}$ es el número de unidades (las unidades son el metro, el kilo, el segundo, el grado, ...), y ${\displaystyle \displaystyle h}$ el rango máximo de la matriz que contiene los coeficientes de las magnitudes de las unidades (a veces coincide el rango de la matriz con el número de variables que tenemos, aunque ésta no es una regla fiable), el número de grupos ${\displaystyle \displaystyle \Pi }$ (o ecuaciones que obtendremos) será ${\displaystyle \displaystyle m-h}$. En el caso que nos ocupa, ${\displaystyle \displaystyle 4-3=1}$ ecuación.

Ahora se cogen las unidades que hemos tomado en nuestro problema y las elevamos a los exponentes que hemos obtenido. Ésa es nuestra ecuación.

${\displaystyle \displaystyle \Pi =h^{-1/2}g^{-1/2}v^{1}m^{0}={\frac {v}{\sqrt {gh}}}}$

(Nótese que ${\displaystyle \displaystyle \Pi }$ es adimensional). Aquí obtenemos aquello que llamábamos "autocorrección": el exponente de la masa es 0, así que desaparece de nuestra ecuación, demostrando una vez más que la caída libre no depende de la masa del objeto en cuestión.

• Paso final: obtención de la ecuación.

${\displaystyle \displaystyle v=k{\sqrt {gh}}}$

con ${\displaystyle \displaystyle k}$ valiendo ${\displaystyle \displaystyle {\sqrt {2}}}$, lo que nos da la fórmula correcta:

${\displaystyle \displaystyle v={\sqrt {2gh}}}$

Principio de Fourier de homegeneidad dimensional[editar]

El principio de Fourier homogeneidad dimensional es un principio de buena formación de las expresiones que relacionan magnitudes físicas de manera algebraica. Es decir, es un principio de consistencia matemática que postula solo es posible sumar o restar entre sí magnitudes físicas de la misma naturaleza. En consecuencia, no podemos sumar longitud con tiempo, o masa con longitud, etc.

Ejemplo[editar]

El principio puede ilustrarse, con el ejemplo, de la energía de un cuerpo que es la suma de su energía cinéticamás su energía potencial:

${\displaystyle E=E_{c}+E_{p}}$

Expresando la energía cinética y potencial tendremos:

${\displaystyle E={\frac {1}{2}}\,m\,v^{2}+m\,g\,h}$

Expresando la velocidad y la aceleración según las magnitudes fundamentales:

${\displaystyle E={\frac {1}{2}}\;m\,\left({\frac {e}{t}}\right)^{2}+m\,{\frac {e}{t^{2}}}\,h}$

Expresado en forma dimensional:

${\displaystyle E={\frac {1}{2}}\,[M][L]^{2}[T]^{-2}+[M][L]^{2}[T]^{-2}}$

Como puede verse tanto la energía cinética: un medio de la masa por la velocidad al cuadrado y la energía potencial: la masa por la gravedad y por la altura, es en ambos casos energía con la misma ecuación dimensional.

Por tanto, este principio de Fourier garantiza la coherencia de una ecuación física. Es importante recordar que si bien las constantes numéricas son adimensionales (ecuación dimensional igual a la unidad), por otro lado las constantes físicas tienen dimensión diferente de la unidad:

e = 2,718281... (base de los logaritmos neperianos) → ${\displaystyle [e]=1}$;

c = 299 792 458 m/s (velocidad de la luz en el vacío) → ${\displaystyle [c]=[v]=LT^{-1}}$

El análisis dimensional es una parte de la física que estudia la forma como se relacionan las magnitudes derivadas con las fundamentales. Tal estudio se hace básicamente para descubrir valores numéricos, a los que los llamaremos "Dimensiones", los cuales aparecen como exponentes de los símbolos de las magnitudes fundamentales.

Fines del análisis dimensional

1. El análisis dimensional sirve para expresar (relacionar) las magnitudes derivadas en términos de las fundamentales.
2. Sirven para comprobar la veracidad o falsedad de las fórmulas físicas, haciendo uso del principio de homogeneidad dimensional.
3. Sirven para deducir nuevas fórmulas a partir de datos experimentales. (Fórmulas Empíricas).

Magnitudes y unidades

Todo aquello que sea susceptible de aceptar una comparación con otra de su misma especie, es una magnitud (con la consideración de que ésta debe ser inmaterial). Así por ejemplo son magnitudes, la longitud, la masa, el tiempo, el área, el volumen, etc.

Llamamos unidad de medida a aquella cantidad elegida como patrón de comparación. Una misma magnitud puede tener varias unidades de medida.

Clasificación de las magnitudes

Por su origen	Por su naturaleza
Fundamentales. Derivadas.	Escalares. Vectoriales.

Magnitudes fundamentales:

Son todas aquellas que tienen la particular característica de estar presente en todos o casi todos los fenómenos físicos, y además sirven de base para escribir o representar las demás magnitudes.

SISTEMA INTERNACIONAL DE UNIDADES (S.I.)
Magnitud	Símbolo	Unidad Básica (Símbolo)
Longitud.	L	Metro (m)
Masa.	M	Kilogramo (kg)
Tiempo.	T	Segundo (s)
Intensidad de corriente eléctrica.	I	Ampere o Amperio (A)
Intensidad Luminosa.	J	Candela (cd)
Temperatura Termodinámica.	q	Kelvin (K)
Cantidad de Sustancia.	N	Mol (mol)

MAGNITUDES AUXILIARES COMPLEMENTARIAS O SUPLEMENTARIAS
Nombre	Unidad Básica (Símbolo)
Ángulo Plano.	Radian (rad).
Ángulo Sólido.	Estereorradián (sr).

Magnitudes derivadas:

En número es el grupo más grande (ilimitado) en el cada uno puede definirse por una combinación de magnitudes fundamentales y/o auxiliares. Estas combinaciones se consiguen mediante las operaciones de multiplicación, división, potenciación y radicación. Por lo tanto toda magnitud derivada tendrá la siguiente forma: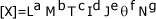 ; donde los exponentes numéricos: a, b, c, d, e, f, g, se conocen como dimensiones.

Ejemplo: área, Volumen, velocidad, aceleración, fuerza, trabajo, energía, calor, etc.

Magnitudes escalares:

Son aquellas magnitudes que quedan perfectamente determinadas o bien definidas con sólo conocer su valor numérico o cantidad y su respectiva unidad de medida.

Ejemplo: área, volumen, longitud, tiempo, trabajo, energía, calor, etc.

Magnitudes vectoriales:

Son aquellas magnitudes que además de conocer su valor numérico y su unidad, se necesita la dirección y sentido para que dicha magnitud quede perfectamente definida o determinada.

Ejemplo: Velocidad, aceleración, fuerza, gravedad, etc.

Múltiplos y submúltiplos

MÚLTIPLOS		SUBMÚLTIPLOS
Nombre y Símbolo	Factor	Nombre y Símbolo	Factor
Yotta (Y)	10 24	Deci (d)	10 -1
Zeta (E)	10 21	Centi (c)	10 -2
Exa (E)	10 18	Mili (m)	10 -3
Peta (P)	10 15	Micro (m)	10 -6
Tera (T)	10 12	Nano (n)	10 -9
Giga (G)	10 9	Pico (p)	10 -12
Mega (M)	10 6	Femto (f)	10 -15
Kilo (k)	1000	Atto (a)	10 -18
Hecto (h)	100	Zepto (z)	10 -21
Deca (da)	10	Yocto (y)	10 -24

Ecuaciones dimensionales

Llamadas también "fórmulas dimensionales", son expresiones matemáticas que colocan a las magnitudes derivadas en función de las fundamentales, utilizando para ello las reglas básicas del álgebra, excepto la suma y resta.

Notación:

A: se lee magnitud "A"; [A]: se lee Ecuación Dimensional de "A".

Propiedades de las ecuaciones dimensionales

1° Principio de Homogeneidad Dimensional o Principio de Fourier (P.H.).

El cual nos indica que cada uno de los términos (monomios) de la ecuación dimensional serán iguales dimensionalmente. (En forma práctica, lo que debemos hacer, es cambiar los signos de SUMA o RESTA por signos de IGUALDAD.

Ejemplo:

En la siguiente ecuación: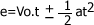 ; luego de aplicar el principio de homogeneidad dimensional nos debe quedar de la siguiente forma: 

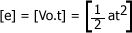2° Términos Adimensionales:

Los números, los ángulos, los logaritmos, las constantes numéricas (como p) y las funciones trigonométricas, se consideran como términos adimensionales porque no tienen dimensiones, pero para los efectos de calculo, se asume que es la unidad, siempre que vayan como coeficientes, de lo contrario se conserva su valor.

3° No se cumplen la suma y la resta algebraica.

Ejemplo:

[X] + [X] + [X] = [X]

[M] - [M] = [M]

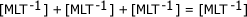4° Todas las ecuaciones dimensionales deben expresarse como productos y nunca dejarse como cocientes.

Ejemplo:

El término: 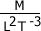, deberá ser expresado como: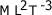 

Fórmulas dimensionales (F.D.) más usuales en el S.I.

Magnitud Derivada	F.D.	Unidad	Tipo
Área o Superficie	L2	m2	E
Volumen o Capacidad	L3	m3	E
Velocidad lineal	LT-1	m/s	V
Aceleración lineal	LT-2	m/s2	V
Aceleración de la Gravedad	LT-2	m/s2	V
Fuerza, Peso, Tensión, Reacción	MLT-2	kg . m/s2 = Newton (N)	V
Torque o Momento	ML2T-2	N . m	V
Trabajo, Energía, Calor	ML2T-2	N . m = Joule (J)	E
Potencia	ML2T-3	Joule/s = Watt (W)	E
Densidad	ML-3	kg/m3	E
Peso específico	ML-2T-2	N/m3	E
Impulso, ímpetu, Impulsión	MLT-1	N . s	V
Cantidad de Movimiento	MLT-1	kg . m/s	V
Presión	ML-1T-2	N/m2 = Pascal (Pa)	E
Periodo	T	s	E
Frecuencia Angular	T-1	s-1 = Hertz (Hz)	E
Velocidad Angular	T-1	rad/s	V
Aceleración Angular	T-2	rad/s2	V
Caudal o Gasto	L3T-1	m3/s	E
Calor Latente específico	L2T-2	cal/g	E
Capacidad Calorífica	ML2T-2q-1	cal/°K	E
Calor Específico	L2T-2q-1	cal/g.°K	E
Carga Eléctrica	IT	A . s = Coulomb (C)	E
Potencial Eléctrico	ML2T-3I-1	J/C = Voltio (V)	E
Resistencia Eléctrica	ML2T-3I-2	V/A = Ohm (W)	E
Intensidad de Campo Eléctrico	MLT-3I-1	N/C	V
Capacidad Eléctrica	M-1L-2T4I2	C/V = Faradio (f)	E
Nota: E = escalar y V = vectorial